Example¶
Here we describe how to use the important functions of the library. If you just want to repeat the experiments, please jump to experiments section Experiments.
Terminology¶
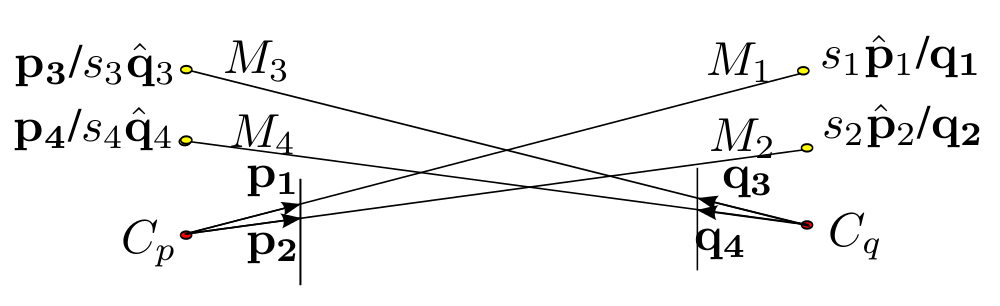
Simplified diagram for the two-camera problem. Assuming the length of respective rays to be \(s_1, s_2, s_3, s_4\) respectively, each marker coordinates can be written in both coordinate frames \(\{p\}\) and \(\{q\}\). For example \(M_1\) is \(s_1\uvect{p}_1\) in frame \(\{p\}\) and \(\vect{q_1}\) in \(\{q\}\), where \(\uvect{p}_1\) unit vector parallel to \(\vect{p}_1\).
We have used the variable names frame1scaled and frame2scaled repeatedly in the code. In the above configuration frame1scaled will be a list of pairs of marker positions that have “scaled” positions in frame “1”. If \(\{p\}\) is assumed to be the frame “1” than frame1scaled will be [(\(s_1\uvect{p}_1\), \(\vect{q}_1\)), (\(s_1\uvect{p}_2\), \(\vect{q}_2\))]
Note that the markers \(M_1, M_2\) are “scaled” in frame 1.
Similarly the frame2scaled represents the rest of the marker position pairs. [(\(\vect{p}_3\), \(s_3\uvect{q}_3\)), (\(\vect{p}_4\), \(s_4\uvect{q}_4\))]
From coordinates with scale ambiguity to rotation translation.¶
This example will walk through computing \(R, t\) from \([(\vect{p}_1, \uvect{q}_1), (\vect{p}_2, \uvect{q}_2), (\uvect{p}_3, \vect{q}_3), (\uvect{p}_4, \vect{q}_4)]\)
Since the polynomials to be solved are too complicated to be solved by hand
and we have different polynomials for different distributions of markers over
the robots. This is why we use symbolic mathematics package sympy to
generate the multi-variate polynomials, eleminating scale varibles to get
single variable polynomials.
Assuming that you have reached the point where you have normalized vectors as shown in the diagram above. The following code will help you compute the scale factors (\(s_1, s_2, s_3, s_4\)).
Let us create an test case. The test case is implemented in
mutloc.test.test_pose_computation. We will try to walk you through the
test case. Suppose there are two marker per camera and the arrangement of
markers is same.:
# Set the absolute position of markers
# M_1, M_2 are fixed on robot L
markersL = [np.array(p) for p in [(-.1, -.1, .3), (.1, -.1, .3)]]
# M_3, M_4 are fixed on robot R
markersR = [np.array(p) for p in [(-.1, -.1, .3), (.1, -.1, .3)]]
Next we choose a random transform between the two robots. We choose a random rotation without any constraints and set translation between 0.7 units and 10 units. Note that minimum translation is set to twice the euclidean distance of he markers considering the arguments given in section III C of the paper; otherwise in a certain rotation configuration the marker of the other robot can be nearer robot’s own markers.:
# Choose a random rotation
quaternion = [random.random() for i in range(4)]
mag = math.sqrt(sum([x**2 for x in quaternion]))
quaternion = [x/mag for x in quaternion]
# Random translation with minimum more than twise the euclidean
# distance of the markers.
translation = [random.uniform(.7, 10) for i in range(3)]
Compute the coordinates of \(M_1, M_2\) in frame 2 and \(M_3, M_4\) in frame 1. These computed coordinates will be normalized to unit vector to simulate perspective projection.
# Christoph Gohlke's transformations.py (included)
import transformations as tf
import mutloc.utils as utils
# Convert to a transform matrix
import transformations as tf
T = tf.quaternion_matrix(quaternion)
T[:3, 3] = translation
# compute the marker positions in the other coordinate frame
# M_3 and M_4 in coordinate frame L
Tinv = utils.transform_inv(T)
frame1scaled = [(utils.apply_transform(Tinv, pR), pR)
for pR in markersR]
# M_1 and M_2 in coordinate frame R
frame2scaled = [(pL, utils.apply_transform(T, pL))
for pL in markersL]
# Normalize computed coordinates to unit vector in order to
# simulate perspective projection
frame1scaled = [(p1 / np.linalg.norm(p1), p2) for p1, p2 in frame1scaled]
frame2scaled = [(p1, p2 / np.linalg.norm(p2)) for p1, p2 in frame2scaled]
Now we feed these arguments to our method
mutloc.core.solve_mutual_localization:
Tgot_roots = corr.solve_mutual_localization(frame1scaled, frame2scaled, tol=TOL)
Their may be multiple roots, but most of low noise situations have only one root as the roots have already been filtered and sorted by error. The first root is the most likely transformation. We can check that this transformation is what we expected.:
self.assertTrue(
np.allclose(Tgot_roots[0], T, atol=TOL),
"Got {0} expected {1}".format(Tgot_roots[0], T))